
Why is pressure sensor accuracy important? From a manufacturer’s point of view, the wrong sensor can cause expensive quality or efficiency problems. This is why it’s important to understand how manufacturers calculate accuracy and recognize what parameters to look at when comparing pressure sensors.
By understanding how manufacturers calculate accuracy, you will be able to make a more informed decision when evaluating pressure sensors. This ensures that the next sensor that you select will have the required accuracy at the right price for the application.
What is accuracy? The International Electrotechnical Commission (IEC) defines accuracy as the “the maximum positive and negative deviation from the specified characteristic curve observed in testing a device under specified conditions and by a specified procedure”. Unfortunately when it comes to defining accuracy for a pressure sensor, it’s more complicated. Accuracy has a large effect on the cost of a pressure sensor and, even more importantly, the quality or efficiency of the process that it measures. It is important to understand what factors determine accuracy and what questions to ask when selecting a sensor.
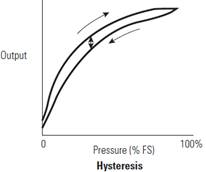
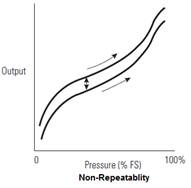
Although though there isn’t a defined standard for pressure sensor accuracy, there is an IEC standard that defines the factors that make up accuracy. IEC 61298-2 states that accuracy must include Hysteresis, Non-Repeatability and Non-Linearity. Hysteresis is the difference between the maximum deviation in the output between consecutive increasing and decreasing full span pressure cycles. Non-Repeatability is the maximum difference in output when the same pressure is applied, consecutively, under the same conditions and approaching from the same direction.
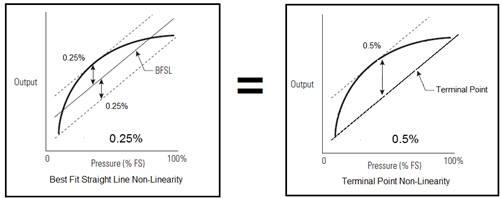
Manufacturers’ definitions of Non-Linearity differentiate. IEC 61298-2 lists three methods of Non-Linearity. The two most popular methods used by sensor manufacturers are the Best Fit Straight Line (BFLS) Non-Linearity and Terminal Point Non-Linearity methods. Usually the non-linearity method used for the sensor will be specified under the sensor accuracy as BFSL or Terminal Point Method. This is why it is important to understand the difference between these two methods. Based on the characteristics of the sensor, it could have two vastly different Non-Linearity percentages. The following diagram shows how the same sensor can have two Non-Linearity percentages.
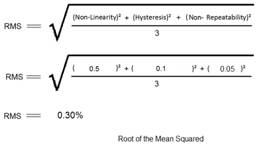
IEC 61298-2 identifies which factors make up accuracy (Non-Linearity, Non-Repeatability, and Hysteresis) but the IEC standard does not define how these factors are combined into a single accuracy. The method in which these values are combined can have a substantial impact on the total accuracy. Some manufactures simply sum the three factors, while other manufacturers use mathematical equations such as Root of the Sum Squared or Root of the Mean Squared to combine them into an overall accuracy. The following examples show how the same transmitter can have three accuracy percentages depending on which equation is used.
Non-Linearity – 0.5% BFSL
Non-Repeatability – 0.05% F.S.
Hysteresis – 0.1% F.S.
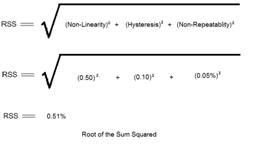
Sum = Non-Linearity + Hysteresis + Non-Repeatability
Sum = 0.5 + 0.1 + 0.05
Sum = 0.65%
Summed Factors
Dwyer Instruments, Inc. specifies an absolute accuracy for its manufactured pressure sensors. This means that the output of a reading of Dwyer Instruments gages or transmitters will fall within a +/- specified accuracy from absolute.

For example, if you have a Pressure Transmitter Series 628 which has a specified accuracy of 1% FS with a range from 0 to 100 psi, any reading that you take from that Series 628 will be within +/- 1 psi from absolute. By specifying our accuracy this way, it makes it easy to check and validate our pressure sensor accuracy. All you need is a reference device with which to compare our sensor to validate the accuracy. For other sensors that use equations to formulate accuracy, it’s much more difficult to validate that the pressure sensor accuracy is correct, because it can vary widely based on which equation has been used to calculate its accuracy.

